FacebookTwitterLinkedInImprimer

Anchor lines, the majority of which are carbon steel cables, are essential components for the stability of offshore floating structures, such as those supporting wind turbines. To overcome the risk of breakage during service, redundant lines are generally incorporated at the design stage, which adds significantly to the cost. The challenge is to improve cable reliability in order to reduce the need for redundant lines, via better prediction of their fatigue life.

Steel cable fatigue is a multi-scale phenomenon. On a large scale, it depends on tension and bending variations associated with stresses exerted by the wind, waves and currents. On a metric scale, behavior depends on friction between the wires making up the cables (Figure 1). Finally, on the millimetric scale of contact between wires, the phenomenon depends on the local mechanical load and the environment (air, seawater, grease).

The approach adopted by IFPEN, in partnership with the LMPS laboratorya at the Ecole Normale Supérieure and the LTDS laboratoryb at the Ecole Centrale Lyon engineering school, consisted in replacing the existing empirical prediction of fatigue resistance with multi-scale modeling based on physics. On a macroscopic scale, the critical zones of the anchor line are determined with aero-servo-hydro-elastic simulationc of the floating structure, which takes into account wind, waves and ocean currents. With variable tension and bending, a load is deduced from a mesoscopic FEMd model (around ten meters) of the cable, which predicts slip and stresses between the wires (Figure 2). On the scale of contact between the wires, modeling makes it possible to verify compliance with a fretting-fatiguee criterion identified experimentally taking into account the environment (Figure 3) and which corresponds to the partial slip/total slip transitionf .

The research conducted has led to significant advances for the simulation of the behavior of steel anchor lines and a better understanding of the fretting-fatigue behavior of the wires contained within them.

For the first aspect, on a mesoscopic scale, the use of the new FEM model generates considerable savings in terms of calculation times. Research currently underway is targeting further decreases through reduced-order modeling via the PGD-LATIN [3] method implemented by LMPS.

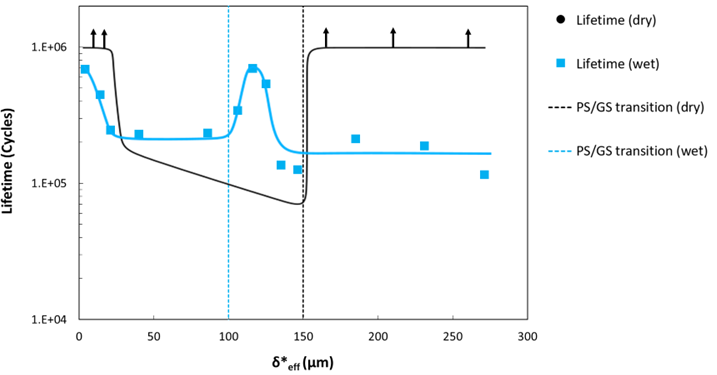
For the second aspect, in addition to highlighting the existence of a critical slip, fretting tests demonstrated the decisive yet complex and sometimes counter-intuitive influence of the surrounding environment. Grease has a positive but limited effect, because its high viscosity limits the penetration into the contact. Seawater has two opposite effects : in one hand it reduces damage by its lubricant properties, in the other hand, it increases it by its corrosive action. Depending on the loading, one or the other mecanism is preponderant (figure 4). The tests in seawater were done in an aerated cell, with control of the electrochemical potential.
  

Fig. 1 : section d’un câble d’ancrage acier
Figure 1: Section of a steel anchor cable


 

Fig. 2 : Modèle éléments finis d’un câble avec contact et frottement [1].
Figure 2: Finite element model of a cable with contact and friction [1].

 

Figure 3 : Essai de fretting-fatigue sur un fil de câble au LTDS [2]
Figure 3: Fretting-fatigue test on a cable wire at the LTDS [2]

 

Figure 4
Figure 4: Fretting-fatigue curves (sliding on x-axis, cycles to failure on y-axis) for steel-steel contact dry (black) and in seawater (blue). PS/GS : « partial slip / gross slip »


a- Laboratoire de Mécanique Paris-Saclay (Paris-Saclay Mechanics Laboratory)
b- Laboratoire de Tribologie et Dynamique des Systèmes (Tribology and System Dynamics Laboratory)
c- Aerodynamic + servo for the controller + hydrodynamic for the immersed elements + elastic for the structure.
d- Finite element model: beam-type in contact with friction in finite rotations and small displacements.
e- Fretting fatigue is the phenomenon on crack initiation and propagation
f- Partial slip: part of the contact surface slips, the other remains stuck; total slip: the entire contact surface slips
  

References:

  1. F. Bussolati, M. Guiton, P.-A. Guidault, O. Allix, and P. Wriggers: Lecture Notes in Application and Computational Mechanics, vol. 93 (2019). 
       
  2. S. Montalvo, S. Fouvry, M. Martinez, F. Ropital, Tribology International, two articles submitted
      
  3. A. Nouy and P. Ladeveze. Multiscale Computational Strategy with Time and Space Homogenization: A Radial-Type Approximation Technique for Solving Microproblems, International Journal for Multiscale Computational Engineering, 2(4), (2004).
    >> DOI: 10.1615/IntJMultCompEng.v2.i4.40 
      

Scientific contacts: martin.guiton@ifpen.fr ; michael.martinez@ifpen.fr ; francois.ropital@ifpen.fr

>> ISSUE  49 OF SCIENCE@IFPEN