Pollutant transport in soils is directly dependent on the heterogeneity of the media present (topology, structure, etc.), which itself is heavily impacted by certain human activities, such as agriculture, industrial operations and mining. The precise description of this phenomenon, across all time scales, can thus prove complex. Yet it is important when it comes to tackling major challenges, such as efficient waste water treatment, or providing access to high-quality drinking water to as many people as possible. In this context, IFPEN’s researchers have been working on methods to gain a better understanding of how pollutants are transported in the underground environment.
Pollutant transport impacted by the heterogeneity of the media
Pollutant transport regimes (transient or asymptotic), as well as the time taken to reach a critical location (for example, an aquifer or a well) are significantly dependent on the underlying heterogeneity of the permeability field. Moreover, in the case of pollutant retention, transport is also characterized by exchange kinetics that depend on local soil properties. This explains why retention times too are spatially heterogeneous.
Two approaches for solute transport modeling
In this research, IFPEN’s researchers focused on the influence of heterogeneous permeability and retention times for transient and asymptotic species transport regimes. Transient regime transport cannot be described by a standard transport equation (Advection-Diffusion equation). This equation only becomes valid in the asymptotic regime.
Researchers began by simulating this transport in a two-dimensional, heterogeneous porous medium. A Mobile-Immobile model1 was used to describe the impact on global solute transfer of mass transfer between the mobile and immobile parts of the medium. This problem was solved using a Lattice Boltzmann method2 [1].
1 This model differs from the classic transport model in that, within the same simulation mesh, it separates the fluid region into mobile (flow and diffusion) and immobile (stagnant) regions with transfer between the mobile part and the immobile part. This transfer follows a first-order kinetics equation.
2 Numerical method employed to solve the Navier-Stokes equation and the advection-diffusion equation using a collision-propagation scheme.
Next, a new one-dimensional random walk model (continuous time random walk, CTRW) was implemented by researchers to determine these transport behaviors on a large scale. The model is based on a spatial Markov model3 for particle speeds, which combines advective-dispersive transport and heterogeneous mass transfer via a Poisson process4. This model, which is on a larger spatial and temporal scale, can be fully parameterized by permeability and flow statistics (without any adjustment parameters) and enables longer numerical simulations to be carried out to reach asymptotic regimes.
3 Stochastic process describing the transition from one state to another.
4 Stochastic process used to describe random events with a certain probability over time.
Assuming a non-linear relationship between local permeability K and local exchange time τ, researchers studied the impact of the Damköhler number (Da, ratio of advection and retention time scales) on the spatial evolution of the solute concentration field.
Fig. 1 shows concentration fields for different Da values [2]. The two mobile concentration fields are very similar, while significant differences can be observed in the immobile concentration fields. In the case of a reliable Da, there are a greater number of depleted regions (dark blue) at the front. In addition, other regions of higher concentration can still be observed a long way behind the front. These two effects result from the heterogeneity in retention time and these regions correspond to high values of this parameter.
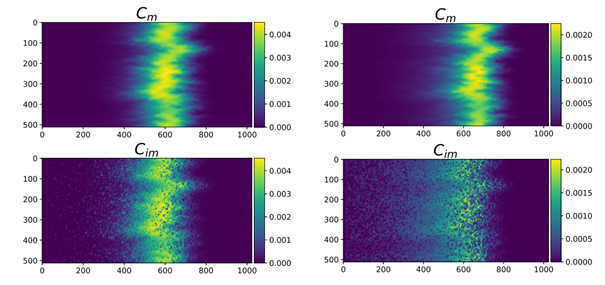
Using CTRW numerical simulations, the researchers also showed that the time required to reach asymptotic regimes in heterogeneous media is, on average, twice as long as for the case of a homogeneous porous medium.
Significant pollutant retention time variability
In conclusion, on the basis of numerical simulations, the researchers showed that pollutant concentrations can sometimes remain in soils for a very long time. This can be explained by the existence of stagnant zones (blue regions, Fig. 1) with high retention times. These zones store and release pollutants over extremely long periods of time.
Moreover, CTRW simulations showed that transient transport regimes may be important, but their correct description requires more sophisticated models. Finally, the results potentially make it possible to explain specific behaviors observed experimentally that cannot be modeled by a standard transport equation.
Consideration of more complex media
As a follow-on from this study, a difficult and ambitious task remains: to simulate pollutant transport in more complex structures, particularly anisotropic or stratified, in order to take into account the highly heterogeneous nature of geological media.
[1] Talon L., Martin J., Rakotomalala N., Salin D. and Yortsos Y., 2003, Lattice BGK simulations of macrodispersion in heterogeneous porous media, Water Resources Research. https://doi.org/10.1029/2002WR001392
[2] Talon, L., Ollivier-Triquet, E., Dentz, M., Bauer, D., 2023. Transient dispersion regimes in heterogeneous porous media: On the impact of spatial heterogeneity in permeability and exchange kinetics in mobile–immobile transport. Advances in Water Ressources. https://doi.org/10.1016/j.advwatres.2023.104425
Scientific contact : daniela.bauer@ifpen.fr
You may also be interested in
Adaptive model for flow simulation in heterogeneous porous media
The calculation of water and gas flows in complex and heterogeneous media is central to technological solutions aimed at tackling current climate and energy challenges.
SC4 - New numerical approach for the characterization of virtual porous materials
Inside porous materials, physico-chemical phenomena such as matter transport, catalytic reactions and capillary effects are strongly influenced by the geometry of the pore networks, i.e., the degree of porosity, the distribution of pore sizes and their connectivity. (....) IFPEN and Saint Gobain Research Provence decided to tackle the problem differently, by exploring a new numerical approach...








