25.11.2024
4 minutes of reading
As is the case with its energy applications, hydrogen production methods are numerous and are widely covered in the literature. Provided this production uses renewable electricity, hydrogen is presented as a promising energy vector to help mitigate climate change [1].
To support the development of this sector, IFPEN joined forces with the Energy Planning Research Center of the Federal University of Rio (UFRJ/COPPE) to develop an economic optimization model for hydrogen production, either by water electrolysis or by steam methane reforming, and with or without carbon capture.
HERA: a model to optimize hydrogen production and transport
The HERA optimization model that was constructed is a mixed-integer linear programming (MILP ) model that takes into account the intermittent nature of renewable electricity production. It was developed using the GAMS language and the CPLEX optimization code. The hydrogen production model developed for the purposes of optimization is illustrated in Figure 1. After compression and storage, hydrogen demand is met by production from either an electrolyzer or a steam reforming unit, with or without CO2 capture. Ethanol, biomethane and natural gas steam reforming were incorporated into the model. The electrolyzer (PEM-Proton Exchange Membrane or Alkaline) can be supplied with renewable electricity and/or electricity from the grid. The objective function to be minimized is the cost of hydrogen production.
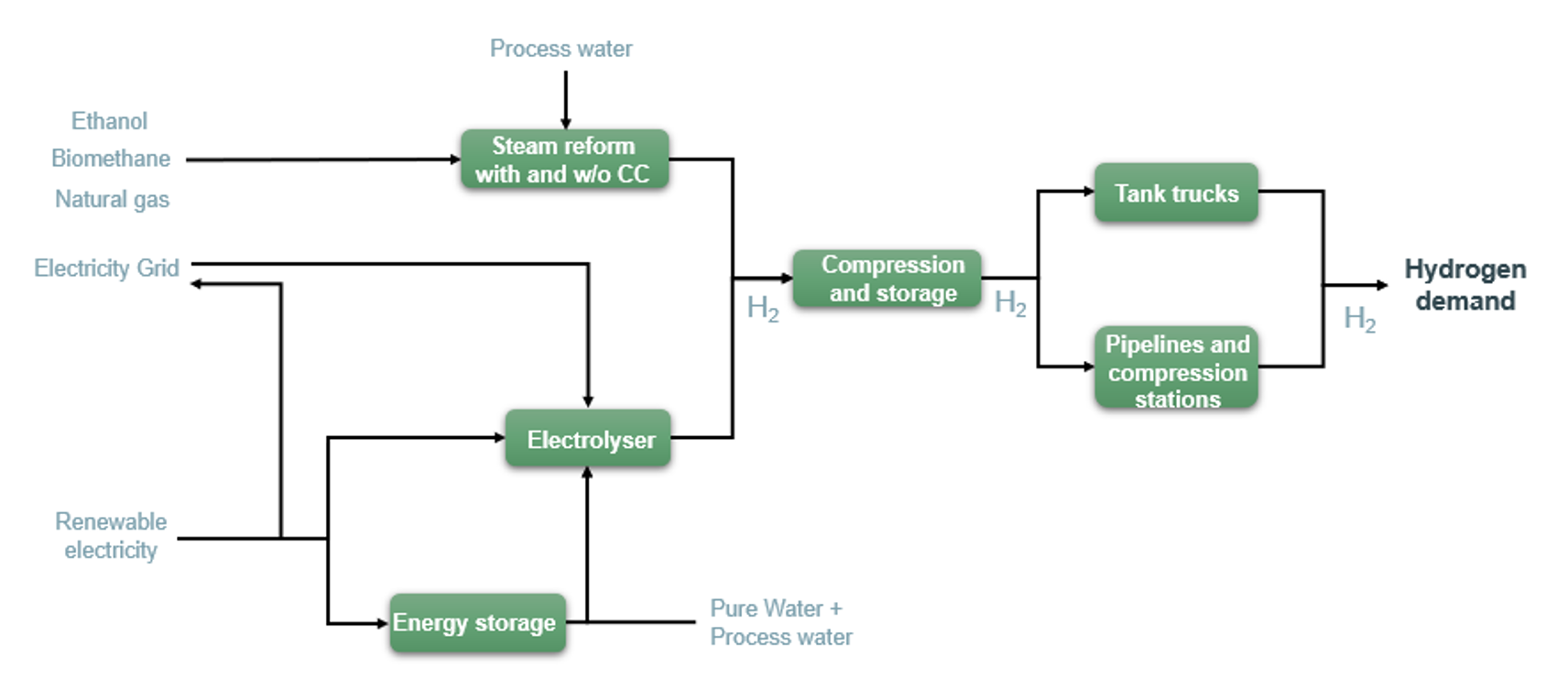
The model is based on matching supply and demand. It aims to meet a demand for hydrogen defined on an hourly time scale. This hydrogen must be produced and transported to the place of use, which requires specific constraints to be introduced to satisfy demand, whether it is transported by pipeline or by truck.
In terms of supply, production comes from available technologies (steam reforming of gas or water electrolysis), the choice of which can be fixed or arbitrated by introducing binary variables into the modeling. The technologies modeled are presented in Table 1.
| Technologies de production | Ressources |
| Steam reforming with or without carbon capture | Hydrocarbons or alcohols (such as natural gas, light petroleum fractions, bioethanol, etc.) |
| Electrolysis (Alkaline or PEM) | Electricity of any origin (hydro, thermal power plant, nuclear, PV, wind, etc.) |
For electrolyzers, as is the case for the steam reforming units, default values are assigned to the fixed and variable cost parameters, which can then be modified by the user. Concerning the renewable energy used, a default number of wind turbines or photovoltaic panel units is defined and can be optimized.
Batteries can be incorporated into the modeling to store intermittent electricity production if doing so means the electrolyzers can be operated at a lower cost.
Hydrogen transport logistics rely on pipelines or tanker trucks, with the choice of transport mode based on cost minimization. In addition, hydrogen storage was considered in the modeling to control production variations from the electrolyzers. Pipeline infrastructure dimensioning modeling is a highly non-linear problem. The choice of pipeline is made from a range of standard diameters and can be reduced to an integer modeling problem. Compressed hydrogen flow in the pipeline was modeled using equations for incompressible fluids. This is recommended for gases with a low flow rate, i.e., with a Mach number less than 0.2 [2, 3]. Where tanker trucks are used, standard logistics costs associated with this mode of road transport are considered.
Hydrogen pressure for transport by pipeline or tanker truck is defined by the user, with a default value proposed. The energy required by the compressors to transport the hydrogen comes from the same sources as the electrolyzer: renewable electricity (potentially with batteries) and the grid. The water required to operate the electrolyzers comes from sea water desalination plants.
The objective function of the minimization problem is a levelized cost function comprising operating costs, annual fixed costs and capital expenditure. Constraints correspond to energy and mass balances, capacity limits and investments to be made, demand to be met, CO2 emission limits, the use of electricity from the grid and potential sales of electricity from “renewable units” to the grid [4,5]. Only whole variables are taken into account in the model, which means that it can be considered as an integer linear programming model. It can be solved as a long-term optimization model for a given year-horizon, or by considering several periods corresponding to successive investment phases.
Case study: a unit for producing hydrogen destined for use in Forteleza, Brazil
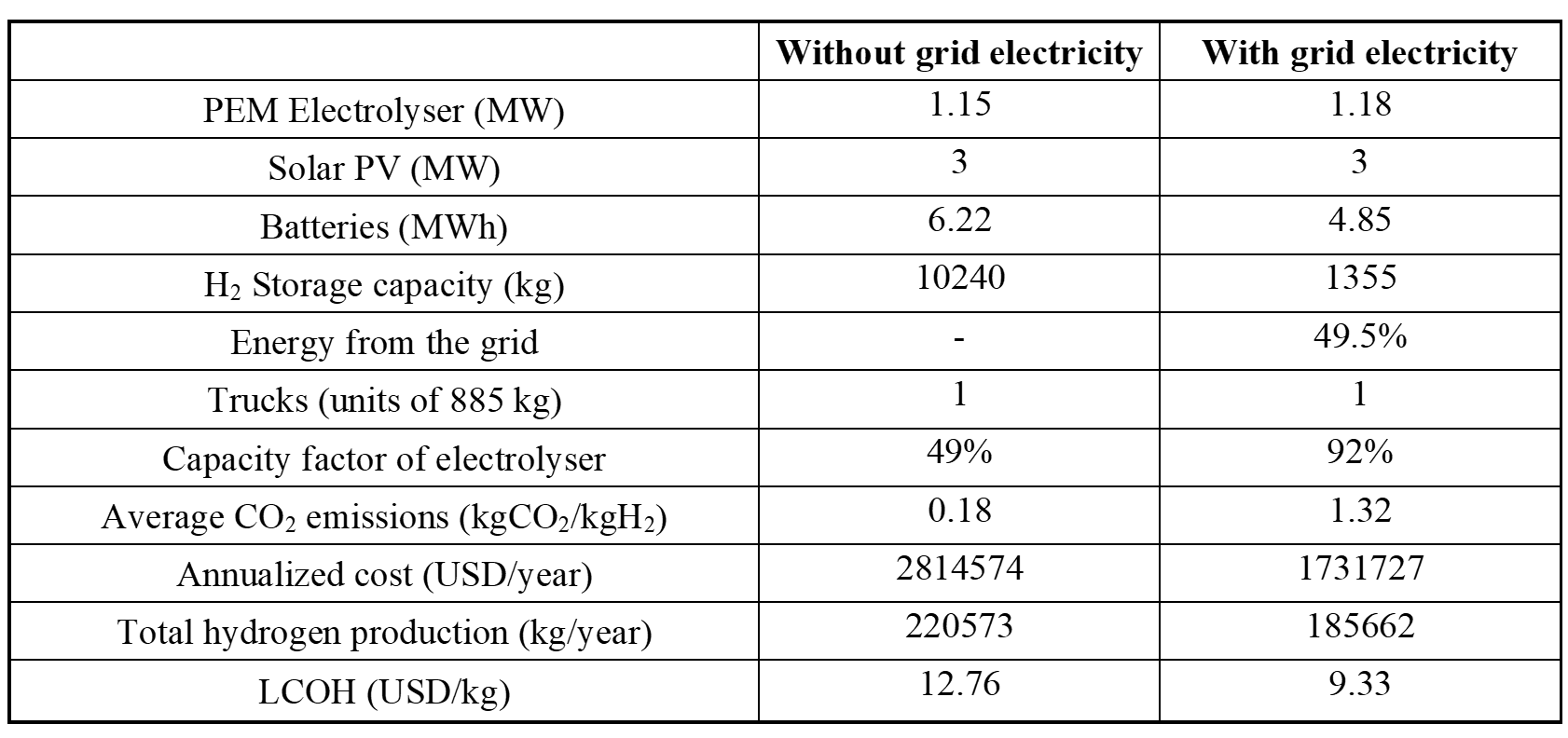
The example described below corresponds to the São Gonçalo do Amarant pilot PEM electrolysis unit, in the state of Ceará, Brazil. The production capacity is 250 Nm3/h of hydrogen, with a photovoltaic (PV) electricity production capacity of 3 MW and a PEM electrolyzer. We are assuming that the hydrogen is destined for Fortaleza, the Ceará State capital, 63 km away. Hydrogen production optimization results are compared for two situations: uniquely with electricity from “PV + battery” units or also using grid electricity. The use of grid electricity to operate the electrolyzer may or may not be authorized.
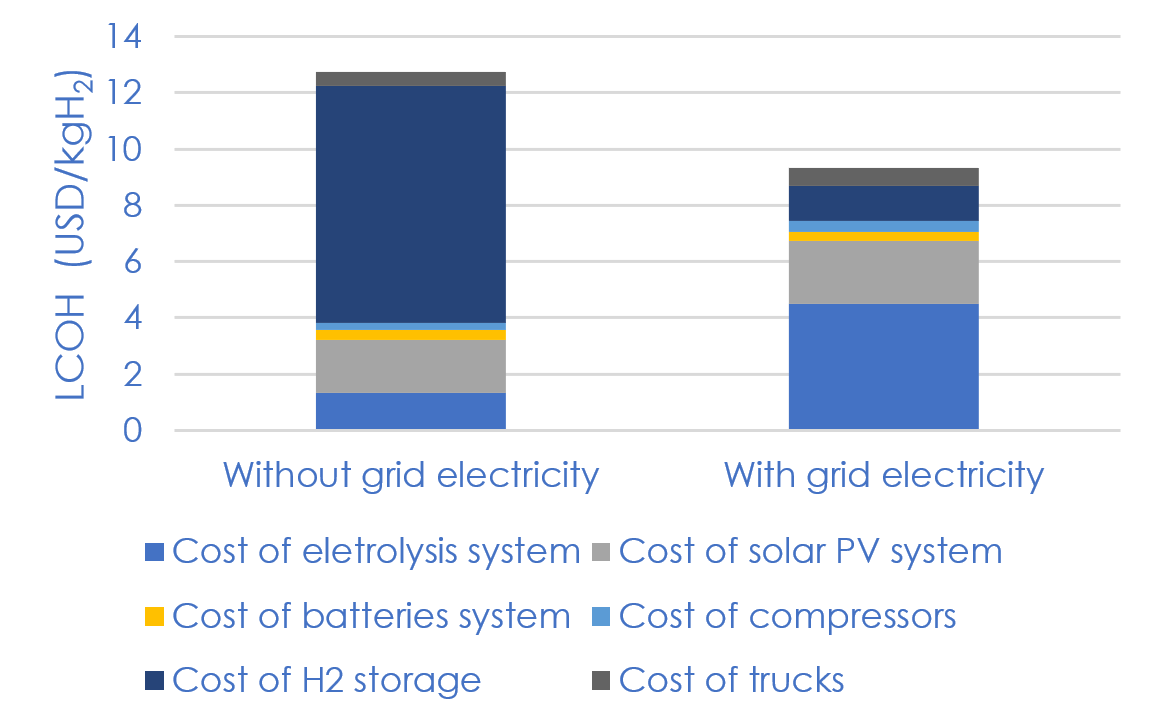
Optimization results (Table 2) make it possible to compare both solutions with comparable electrolyzer capacities: 1.15 MW in the solution without grid electricity and 1.18 MW with the use of the grid. The hydrogen storage capacities required to meet demand are considerably lower (1,355 kg compared to 10,240kg) in the case where grid electricity is used: this greater storage requirement results from recourse to a “PV + battery” combination. Hence, the levelized costs of hydrogen (LCOH) appears to be significantly lower in the grid scenario: 9.33 USD/kgH2 compared to 12.76 USD/kgH2 (Figure 2).
Towards a decision-making tool
In conclusion, the use of this modeling approach plays a crucial role in optimizing hydrogen production design and supporting the energy planning decisions of investors and policy-makers alike. The results can help highlight the impact of various taxes, subsidies and specific policies on the development of hydrogen markets, and support the development of associated regulations.
References:
[1] International Energy Agency (2023) “Global Hydrogen Review 2023”, Global Hydrogen Review 2023. 176 p.
[2] Darbandi, M.,Schneider, G. E. (1998) “Analogy-based method for solving compressible and incompressible flows”, Journal of Thermophysics and Heat Transfer, 12(2), p. 239–247.
>> https://doi.org/10.2514/2.6327
[3] Guerra, J.,Gustafsson, B. (1986) “A numerical method for incompressible and compressible flow problems with smooth solutions”, Journal of Computational Physics, 63(2), p. 377–397.
>> https://doi.org/10.1016/0021-9991(86)90200-7
[4] Nascimento Da Silva G., Lantz F. Rochedo P., Szklow A. (2023), Hera – Hydrogen economics and infrastructures optimization, IFPEN Research paper - Cahier de l’Economie n°155, Juin 2023
>> https://ifp.hal.science/hal-04147420v1
[5] Nascimento da Silva G., Lantz F., Rochedo P., Szklo A. (2024), Developing and applying the Hydrogen Economics and infRAstructure optimization model (HERA), International Journal of Hydrogen Energy, 61, pp. 1170-1186
>> https://doi.org/10.1016/j.ijhydene.2024.02.015
Scientific contact: Frédéric LANTZ





